これまでの議論「弧理論への入り口(自然科学は間違っている)」において、数学者岡潔は「時間」が問題であると述べました。(過去記事を参照) そして、時間を含んでいる光速度cを中心に据えてしまった相対性理論は誤りです。 詰まるところ自然科学は、「運動は時間より求め、時間は運動より求めている」からに他ならず、古典的時間の概念を事象の地平面である天文学や相対性理論の補正を施した素粒子理論に適用することは、誤りで、彼らは正しいエネルギー値を示していないという結論でした。
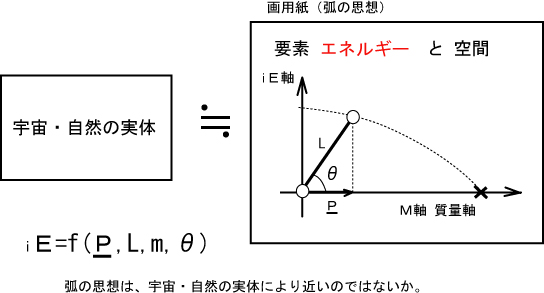
で、弧理論(Ark Theory)の考え方によれば、エネルギー値は直接には求められずE軸上の実体が「積分を伴う投影」によって、我々の住むM軸に質量mと運動Pが生じると考えています。第3起電力のエネルギー源について(考察)を参照。
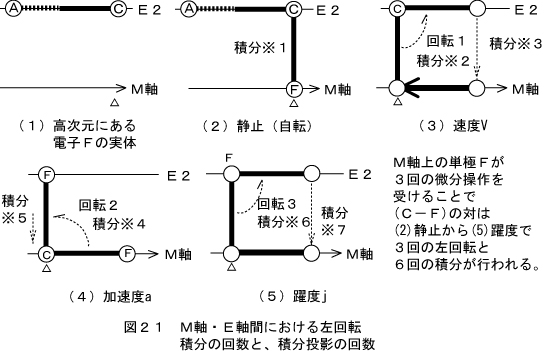
E軸上にある実体は、積分を伴ってM軸に投影されることで、例えば電子の質量や電荷、あるいは周囲の様々なポテンシャルが生じると考える訳です。 すると、最初の第1回の積分を伴う投影によって、M軸上に質量等が現れて、超効率インバーター「デゴイチ」のトランス内部には、都合第1回から数えて7回の積分が行われることになります。
最初の1回を除くと6回の積分を伴う投影と回転が、E軸とM軸の間で繰り返されることによって、M軸上に「距離の7乗に逆比例する力」が現れるというのが第3起電力の考察の骨子でした。(この力場はレンズ状をしていることも分かりました。) そして、肝心なのはM軸に現れる現象は「積分を伴う」わけで、積分に2.8回とか3.48回などというものはありません。 ですから、M軸即ち、3次元物理空間に現れる現象は、全て「整数」であることになります。 整数とは、つまり現象は「離散的に現れる」ということを意味します。 極微小な領域での現象が離散的であることは、よく知られています。 結局、弧理論(Ark Theory)の考え方によるE軸-M軸の複素数空間では、M軸(3次元空間)に現れる物理現象は微小な領域において、離散的にならざるを得ないということです。
この考察を踏まえて「第3起電力の考察」の補遺1「ゼータ関数との類似性と数体系」(pdf版ではp73)について考えます。 この補遺では、弧理論(Ark Theory)によるE軸-M軸の複素数空間は、リーマン予想のゼータ関数に似ているとしました。 今、M軸に現れる現象が離散的であることの理由が、「積分を伴う投影」であり、物理現象は基本的に「整数」に起因すると考察するならば、E軸-M軸の複素数空間を基本とする弧の考え方は、リーマン予想におけるゼータ関数にそっくりということが、更にいえるという結論になります。 というより、そのものです。 ですから、素数が原子核のエネルギー準位と関係があるというのは、もう少し先の話です。 ましてや、12進法の数学が宇宙に馴染むというのは驚異という他ありません。
物理現象が離散的であることの理由は、量子理論からは説明が付かないのは明かです。約100年前に放棄したのですから。