過去記事に（物理現象は「整数」である）と書きました。関連したことを少し書きます。
相変わらず単極誘導について研究しているのですけれど、先日、直流モーターがほしかったのでＦＤドライブを分解したところ、
ブラシレスモーター
古い型のブラシレスモーターが出てきました。余りにも綺麗なので写真を撮りました。現在ではもっと小型のモーターが使われているでしょうけれど、それよりＦＤ自体が滅多に使われなくなりました。 コイルは機械捲きなのでしょうか、綺麗ですね。 ところで、このブラシレスモーターの磁極は１５あります。ステーターの数は６や９、あるいは１２などがあり、制御のための極数は２、３、あるいは４極などがあるようです。
問題は、磁極やステーターの数についてです。 モーターの回転をスムーズに制御するには、２、３、６、９、１２などが都合良いようです。 これまで管理者が展開してきた弧理論（Ark Theory）に引用する、ある科学者の言葉に次のようなものがあります。
「十二進法を基礎としたシステムがもっとかんたんで有用で、本質的により可分性があるとわかったんだ、知ってのとおり十二は、二、三、四、六で割り切れるが十〇は二と五でしか割れないんだ。」
なぜ、突然に素数の話をするのか訳が分からないものの、何か引っかかるものがありました。 研究を続ける内に、弧理論での模型図が
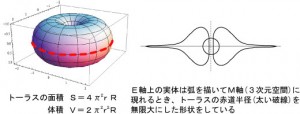
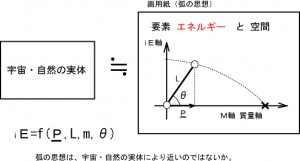リーマン予想に出てくるゼータ関数にそっくりだということに気付きました。 エネルギー軸上の実体が我々のいるＭ軸上に（積分を伴う回転により）投影される仕組みは、ゼータ関数そのものです。 ただ、ゼータ関数の横軸は整数ですから、意味が分かりませんでした。 ところが、弧理論の仮説には、「積分と回転を伴う」というのがあります。 積分の回数に実数はあり得ないことに気付きました。ですから、弧理論の考え方によれば、物理現象は当然のこと「整数」なのですし、実際、微小な領域での現象は、離散的な訳です。 Ｍ軸上の物理現象は、Ｅ軸上の実体へ、次いでＥ軸上の実体の変化は、Ｍ軸上へ投影されます。この間、回転と積分が繰り返されます。 例えば、電気は磁気に磁気は電気に９０度、変化して現れます。
超効率インバーター「デゴイチ」での第３起電力仮説を弧理論の考え方で説明するとき、都合、最初の積分投影から数えて７回の積分があります。（第３起電力のエネルギー源についてを参照） インバーターのコイルにパルスを印加することで、最初の１回を除いて、６回の積分が繰り返されることで、パルス頂点が持つ躍度（jerk）は、磁力線と順方向に現れて、コイルに流れる電流の方向へ捻れながら、無限遠に消失する（レンズ状の場を持っている）らしいことが分かってきました。このときの場の力が「距離の７乗に逆比例する力」であった訳です。
ですから、物理現象は「整数」であり、かつ「３次元空間の角度を整数で分割」ものとして現れるらしいことが推測できます。では、いくつで分割すればよいのかが問題となります。その正解が上記の科学者の言葉であるならば１２進法で分割すべきだと気が付きます。 冒頭のブラシレスモーターの例にあるように、私たちは半ば無意識のうちに１２を基本とする分割を角度に適用していることになります。
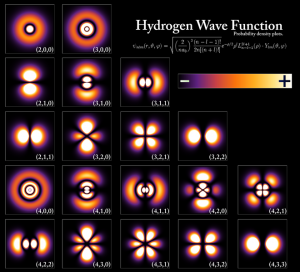
上図は、水素の原子模型です。図は確率分布として描かれていますけれど、核を中心として整数に分割されていることが分かります。 Ｅ軸からＭ軸へ投影されるときの３次元形状が未だ分かりませんけれど、投影された質量ｍと運動Ｐの関係及び真のエネルギー値iＥとの関係が理解できれば、Ｍ軸上での形状が理解できるようになる気がします。 数学ができて「πやe」で表現した方が何か格好いいですけれど、管理者がある科学者の言葉に従って１２進法の数学に変えよう（弧電磁気論のあとがき）と主張する根拠はご理解いただけるでしょうか。 結局のところ、物理現象は整数であり、かつ１２を基本とした数にもっとも馴染むということです。
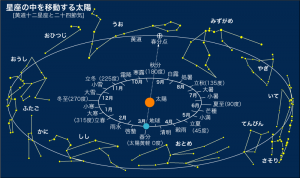
ここからは、管理者の妄想です。 なぜ、現代において、時間や角度に１２を基本として使うのか？いつから使うようになったのでしょうか？例えば１ダース１２というのもあります。 地球の文明は、いくつも作っては壊されてきたといいます。前回の文明の崩壊の危機において、人は最期に何を残すと思われますか。 文明崩壊後の彼らの子孫（つまり現代の私たちの祖先：たとえばシュメール文明）は放射能の影響によって急速に原始化するでしょう。 そういう私たちの祖先に、１２進法の大切さを残すためには、口伝（口承）に頼るしかないと考えたのではないでしょうか。 羊飼いや農耕民の口伝において星座が１２であれば、季節（時刻）も１２で分割するでしょう。 なんだか漠とした話ですけれど、分かるような気がします。
Follow me!
