電磁気現象 の内、ファラデーの単極誘導の現象について、過去250本以上の記事を書いてきました。参考記事です。(本記事は読みにくいですが、ご辛抱ください。)
- 2015年6月12日 ”電磁誘導” と ”単極誘導” は異なる現象である。 (より高い対称性について)
- 2018年1月8日 「ファラデーの 単極誘導モーター に生じる力」を調べるに「ローレンツ力」という言葉を用いない理由
- 2025年7月18日 単極誘導 ≠ ローレンツ力 実は楕円双極が正解
- 2025年10月14日 ローレンツ力は、ファラデーの 単極誘導 とは別もの
電磁気現象を物と事にわける
どうも、 電磁気現象 は物と事の両方にまたがって現れる現象です。ただ 電磁気現象 には、教科書で示されるより、高い対称性があると考えてきました。
その前に前提です。
- ヒトがわかるのは物と事(動き:運動)
 図1
図1 - 物と事が揃って、初めて言葉で言える
- 物には量、事には質がある
- 言葉には「1、2、3、4」と言った数がある
- 数には2種類ある(物の量にかかる数、事の質にかかる数)
ここで、電磁気現象を出来るだけ、物と事に分けてみましょう。
電磁気学は電子の挙動に関して記述しています。但し、電磁気学が成立した19世紀後半において、原子の構造はわかっていませんでした。
- 電子は物である
- 電子が持つ電荷 → 電場(電界)
- 電子の運動 → 磁場(磁界)
- 特徴として、必ず直交して現れる
- 運動から時間を作る
- 従って、磁場は時間と関係する
ここで、電子、電荷、電場、磁場を物と事にわけますが、実際のところよくわかりません。但し、電気磁気現象において、物は単極ですし、事は双極です。
- 電子は物(単極)
- 電子の電荷は物に付随する事
- だから、電場は単極ながら、電子にかかる事
- 運動する電子は周囲に磁場を持つ
- 磁場は双極であり、事
電場と磁場は必ず直交して現れます。
- 電場(単極)⊥磁場(双極)
- いずれも電子に付随する事
それで、電磁誘導は、電気と磁気が現れる関係(⊥)を示しています。
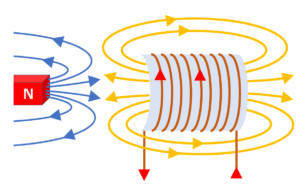
動画1 電磁誘導における作用と反作用 (往復運動、振動運動)
ここまでが、電磁気現象の内、電磁誘導についての説明です。誤りがあればご指摘ください。
単極誘導の力学的な特性
電磁誘導は図1の通りですし、力学的な特性は動画1に示すとおりです。ご存知の通り電磁誘導は銅線、コイル、あるいは磁石との間に生じます。
一方で、ファラデーが発見した単極誘導の現象(主に単極モーター{電動機}の力学的な特性)は、次のようでした。
- 必ず回転運動である
- 力は接点(ブラシ、電極)に生じているようだ
- だから、磁石は生じる力と無関係(ファラデーのパラドックスと呼ばれる)
- 力は磁石の重心位置が最も強い
- 力は磁石の磁束密度に比例する傾向にあるが、寧ろ磁石の質量に比例する傾向にある(内容は省略します。)
実験による説明
参考となる動画を3つ挙げます。Show Ark(@kodenjiki)チャンネルの再生リスト、実験タブからです。
次の動画において、ファラデーのパラドックスを見ることが出来ます。
動画2 単極誘導モーター(水銀の渦に乗る磁石)20150601
動画3 単極誘導モーター実験1-4
磁石は水銀、銅円板の動きと力学的に無関係です。勿論、近傍に磁石がないと水銀や銅円板に回転運動(単極モーター)は起きません。
また、動画3において、銅円板の回転の反作用はスズメッキ線が受けています。他の実験でも確かめていますが、一部の放電実験において疑義があります。
動画4 単極誘導モーター 実験8-1

写真1 実験8-1 左から、ブレッドボードに組んだタイマー(通電3秒)、DC電源、ガウスメーター、タコメーター
アルニコ磁石に薄い銅板を巻いて磁極部分に回転軸を取り付けたものです。生じる力を定量的に示す為に回転数を測りました。
図に示すとおり生じる力は、磁石の重心位置(中央付近)において最大です。但し、アルニコ磁石の磁束は必ずしも軸対称、点対称ではありませんし、そもそも磁束を切るローレンツ力という説明と一致しません。
電磁誘導と単極誘導の現象は直交する
電磁誘導は磁束で説明されます。
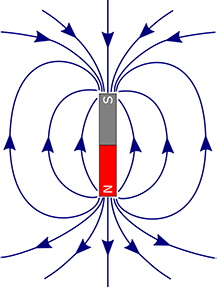
図4 磁気双極 磁界(磁場)出所失念
一方で、井出治氏によるパルストランスついて考えました。
今思うと半完成でしたが、その結果行き着いたのが発散トーラスでした。
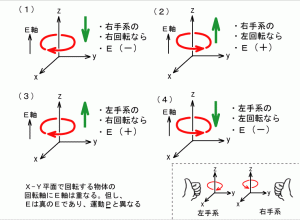
図5 4種類の発散トーラス(右手系、左手系、上向き、下向き)
これの内、2つを組み合わせたのが楕円双極(右回転、左回転がある。)です。
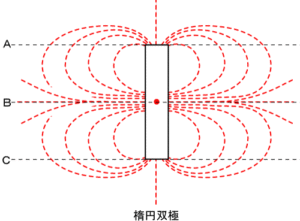
図6 楕円双極の断面
図は横からです。但し、上から見た図はまだ出来ておりません。断面A、B、Cのいずれも渦(回転:トーション:ねじれ)を成していますが、最も強いのはBです。現在のところ立体的な形状を想像するしかありません。
一応上から見た図(仮)を示します。
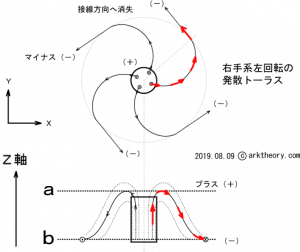
図7 発散トーラスの例(右手系左回転)
図5と比較して想像してください。2つを重ねると互いに打ち消し合って双極を作ります。模式的に例を示します。

写真2 図6は図5を組み合わせて出来る(右手系左回転(+)と左手系左回転(-)は打ち消しあって双極を作る)
その上で、図4(磁気双極)と図6(楕円双極)を重ねます。
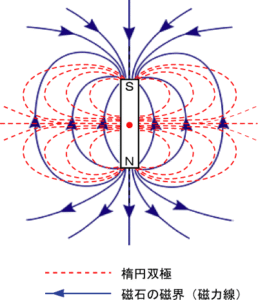
図8
- 電磁誘導⊥磁気双極
電磁誘導は双極(線対称)です。これを90度ずらして置いたのが楕円双極(赤い破線)だと気づきます。但し、楕円双極の形状は双極ですけれども、磁石の内部において点対称です。
どうも実験の結果、楕円双極は単極誘導の現象と同じだとの感触を持っています。
- 電磁誘導は往復運動(往復:振動)
- 単極誘導は回転運動(円運動)
電磁誘導の{往復(振動)}現象と単挙誘導の{回転(円)}現象の違いはありますが、過去に記した「より高い対称性」だとわかります。
- 電磁誘導⊥ファラデーの単極誘導
つまり、図8のとおりならば、次が言えます。
- ファラデーの単極誘導は図6の磁気双極による
要は、電磁誘導と単極誘導は別の現象であって、電磁誘導は磁束(磁界)によるし、ファラデーの単極誘導は磁気双極によると考えられます。そして、磁気双極の元は4種類の発散トーラスです。
以上の考えに矛盾しないように思える実験がありますのでリンクします。
電磁気現象 は「物と事」の両方にまたがる
まとめます。電気磁気現象は「物と事」にわけますと、かなり複雑に入り組んでいることがわかります。
単極、双極、それぞれに特性があって、時間との関係が密にあります。それで押し並べて言えるのは、 電気磁気現象 は物と事の両方にまたがって現れていると言うことです。
重力は電磁気現象の隣にある
管理人の直感によれば、「重力はもっと高い対称性」の範囲にあるだろうと感じます。
ここで、3つの現象(電磁誘導、単極誘導、重力)を比較します。
- 電磁誘導が示す往復運動・振動(任意の加速度運動)
- 単極誘導が示す回転運動(渦:加速度一定の特別の場合)
- 重力の特性(加速度一定)
こう考えると、重力の加速度一定という性質は、回転運動(渦)に起因すると考えられます。それも加速度運動の内の特別の場合の範囲に入るようです。
すると「単極誘導の現象は、重力と直交する」という考えに至ります。
- 電磁誘導(振動・往復現象)⊥ 単極誘導(回転運動)⊥重力
やはり、「加速度運動には区別できないが、幾つかの種類がある」と考えざるを得ません。しかも、「それぞれの加速度は区別できないが、互いに直交している」ようです。
思いつく加速度の範囲を図にします。
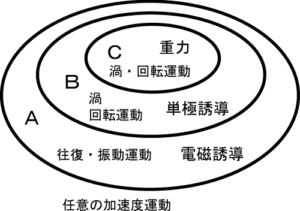
図9 加速度運動
物質・物体に加速度が働きます。これを力と言います。これは任意です。
その内、電磁気現象に関連する加速度をAで示します。Aは往復運動、振動です。これが電磁誘導です。これとは別に単極誘導をBに示します。Bは本質的な回転運動(渦)ですして、加速度は一定です。
一見、無関係に見える重力はCです。重力は加速度一定の回転運動に起因すると考えるならば、Bと似ています。
それで、それぞれは空間的に直交していますから、双極であったり、単極であったりします。因みに重力は単極ですが、事(動き:運動)です。それぞれの関係を示します。
- 磁石は双極
- 電磁誘導は往復運動(双極)
- 単極誘導は回転運動(単極)
- 重力は回転運動(単極)
そう言えば、地球は磁石の性質を持っています。