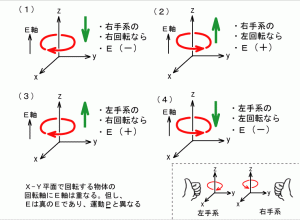
先日の記事にて、単極誘導の現象と 重力 は直交しているとの考察を示しました。
- 2025年11月1日 電磁気現象 は「物と事」の両方にまたがる（重力との関係を考察する）
電磁誘導と単極誘導は直交
前回の復習を兼ねて説明します。電磁誘導と磁石の磁場（磁界）との関係は以下です。
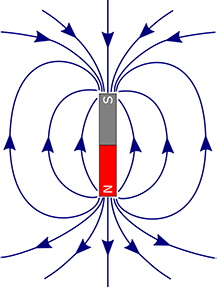
図１ 磁石が持つ磁場
これに対して、実験で確かめた単極誘導の性質をまとめると、（多分）楕円双極によるとしました。
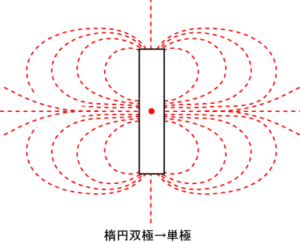
図２ 磁石が持つ楕円双極（4種類の発散トーラスの内、2つを組み合わせて出来る 右回転と左回転がある）
丁度、磁石を取り巻く力線は２種類あって、図１に図２を重ねたものの様です。
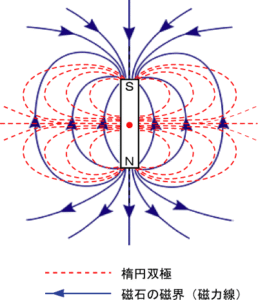
図３ ２つはほぼ区別できないが、各々独立して存在する 楕円双極は電子と原子核との相互作用
- 電磁誘導（磁場） ⊥ 単極誘導（楕円双極）
但し、単極誘導の現象は、本質的な回転運動（円運動）です。一方で電磁誘導は、往復運動（吸引と反発、振動）の現象で、力は回路に生じます。
単極誘導と重力の類似性
ファラデーの単極誘導の性質をまとめます。
- 回転運動（加速度は一定）
- 回転させる機構がない（回る）
- 力は接点で生じている
- 磁石の重心位置での力が最も強い点対称
- （恐らくは）原子核との相互作用
この加速度一定で、かつ点対称という性質から、重力（加速度一定な点対称）は回転運動に起因すると推測ました。ということで、単極誘導の現象と重力は極近い関係にあると考察しました。
- 単極誘導 ⊥ 重力
弧理論は４次元の理論
ここで本題です。この直交とはどう言った状態を意味するかです。弧理論を一言で言います。
- 自然は別の次元軸からの投影による影像である
別の次元軸を基軸、あるいは気軸と言います。Ｋ軸とします。投影による影像をＭ軸、物質軸と言います。言わば、弧理論はＭ軸３次元にＫ軸を加えた４次元の理論です。
但し、時間は物の運動Ｐから作りますので、Ｍ軸内での事に過ぎません。時間に次元軸はありませんので注意です。
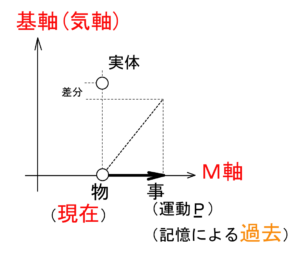図３
よく知られているようにＭ軸の次元は（x、y、z）で表されます。その関係は以下です。
- x ⊥ y
- y ⊥ z
- z ⊥ x
それで、上記の通り電磁誘導と単極誘導はＭ軸において直交です。
それでは、重力はというと弧理論では以下です。
- 重力は投影元であるＫ軸が原因
- Ｍ軸での全ての現象の原因はＫ軸にある
単極誘導の原因も重力の原因も基軸（Ｋ軸）にあります。そして、原子核との相互作用である単極誘導と重力は４次元的に直交する関係にありそうです。
発散トーラスはＫ軸とＭ軸にまたがった存在
しかしながら、ここまでに発散トーラスを組み合わせた楕円双極によって起きる単極誘導の現象がなぜ重力と関係があると考えるのかの根拠を示していませんでした。
- ４種類の発散トーラスは、いずれもＭ軸とＫ軸の両方にまたがった存在
- 内、２種類を組み合わせることによって、図２に示した楕円の双極になる
- ２つの発散トーラスは、互いに打ち消し合うことによってＫ軸との縁が切れる
- 結果、Ｍ軸上での現象（単極誘導）となる
- 互いに打ち消し合って現れる現象を言い換えると「現象は差分に過ぎない」と言うこと
発散トーラスは４種類あります。
図４
これらは、基本形が双極でありながら、片方はＭ軸上にあり、もう一方はＫ軸につながっています。これによって、発散トーラスはＭ軸上で単極の様に振る舞います（但し、物ではなくて事です。）がしかし、もう一方の極の位置はありません。
この性質を持つ発散トーラス２つを組み合わせることによって、双極の形状と性質を持つ楕円双極（図２）になります。
４次元の直交
問題は４次元的な直交をどう表すかです。数学に使われる記号の正確な数は不明ですが、２００か３００以上あるようです。
それでも適切な記号はありそうもないので２つの候補を考えました。
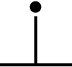
図５ 候補１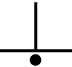 
図６ 候補２
いずれも、Ｍ軸においての直交にプラスする意味合いで●を付けました。この記号によって、Ｍ軸とＫ軸の間の直交を示すことにします。
ただ●印を使うには理由があります。かつて自費出版した弧電磁気論の足跡の解析によって、直交を表すに●の印が使われていたからです。
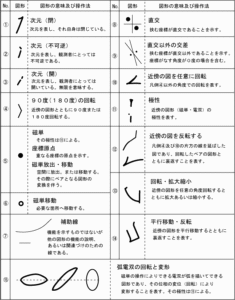
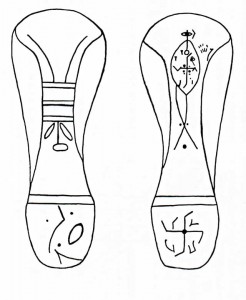図７ 図中に示される●の印は直交等を意味する
図７の解析による凡例を以下に示します。
図８ 弧電磁気論ｐ５５図３８凡例
図８の右上No.⑧の大きい●がそれです。
兎に角、ファラデーの単極誘導は４次元的に重力と直交していると考えます。
- 単極誘導 重力
２つの間の橋渡しをしているのが発散トーラスです。前述の通り、打ち消しあった差分が単極誘導の現象であることに注意です。
では、重力とは何か、なぜ起きるのかを次に説明します。
重力とは基軸での回転運動
弧理論で言えば、重力は基軸を中心とする渦（回転運動）です。水と油の境界面の模型により示します。
gif１ 渦には凹凸と左右がある
境界面がＭ軸です。Ｍ軸に直交する渦が原因となってＭ軸に勾配が現れます。これが重力です。
それで、重力もまた模型で示す事が出来ます。
動画１ 引力と斥力
動画の１円玉とアルミホイルにより出来る表面の凹凸がgif１に示した渦（回転運動）によって出来る勾配に等しいです。
以上をまとめますと次です。
- Ｋ軸上での渦（回転運動）∝Ｋ軸での凹凸（勾配）∝ Ｍ軸での引力・斥力＝重力
補足しますと、弧理論による質量はＫ軸上での渦の動かしにくさです。渦（回転運動）の結果が重力ですから、質量と重力には比例の関係が成り立ちます。渦の動かしにくさは経験的によくわかっています。
Follow me!
