２０１７年５月２４日の記事「 発散トーラス の性質について」に続いて発散トーラスによる 重力 について説明します。その前にこれまでの考察を振り返ります。
- 自然科学の枠組み「時間･空間」は自然そのものではない。簡単な模型である。
- 時間は運動から作る。
- 運動は空間の性質の一部である。（空間に物質が存在し運動していると考える）
- 時間は空間の持つ性質の一部から作ったものである。
- 時間は過ぎ行く運動の記憶である。（人が持つ観念に過ぎない）
- 時間は、運動の現在を含まない。（時間は過ぎてからしか知り得ない）
- 従って、古典力学・量子力学とも決定論になり得ない。（確率とも精度の話しでもない）
- だから自然科学の「時間・空間」という枠組みは間違っている。（空間という枠組みならまだよい）
- 自然科学は、時計という装置の運動と被測定物の運動を比較しているに過ぎない。
- 量子力学にかかる無限大の問題は「９.」に原因があるのではないか。
Ｅ＝ｍｃ２について、「物質→エネルギー、エネルギー→物質」へ転換するとされるが本当は一つの実体の異なる面に過ぎない。言い換えると物質もエネルギーも別の次元軸に在る実体が投影されることによって現れる映像であるということです。これが別の次元軸を考える根拠です。 少なくとも自然科学では自然が存在ではないことがわかっています。
発散トーラスには次の４つがあります。
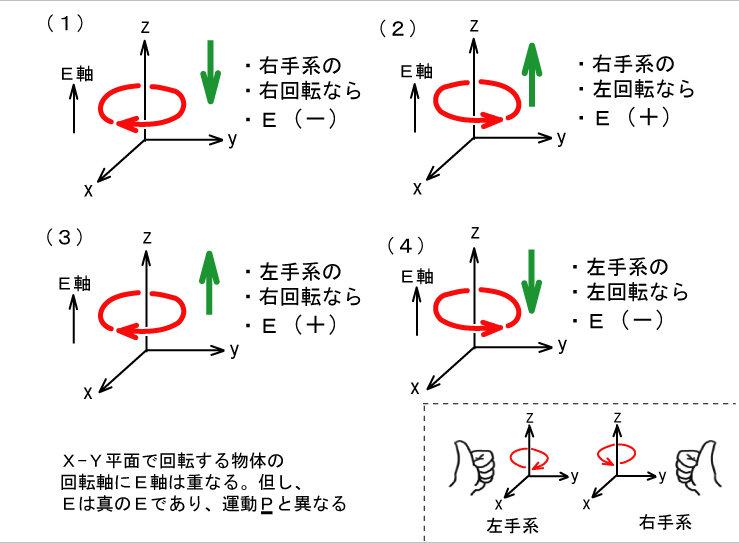図１
右下図に注目します。例えば、右手形ならば反時計方向の回転でかつｚ軸方向に親指が来ます。つまり、左回転でｚ軸方向の（＋）方向にＥ軸が重なります。これは図１の（２）に相当します。
発散トーラスの形状は次のようでした。
改めて図に示すと
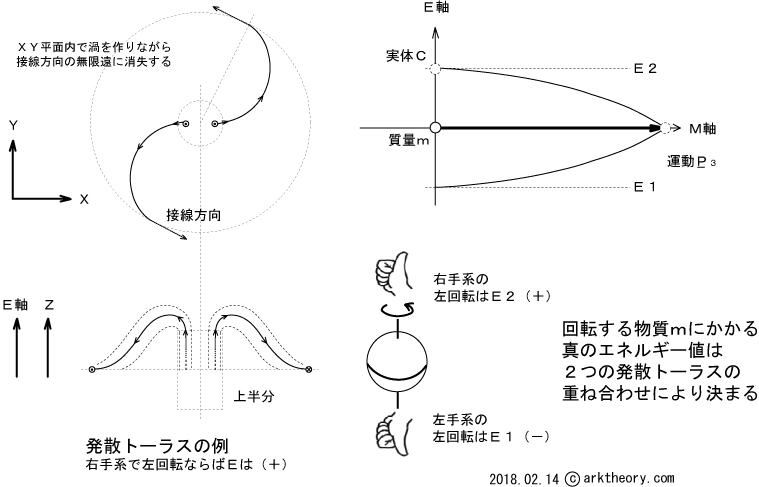図２
の左になります。左上は、発散トーラスを上から観た様子です。左下図は、その断面です。極の方向へ出て外縁部へ向きを変えて渦を描きながら消失します。極めて強いが到達距離の短い「距離の７乗に逆比例する力」と理解しています。この左図の発散トーラスを右上図のＥ－Ｍ軸平面で示すとＥ２の弧になります。
ところで、回転する物体には図１の発散トーラスの内、必ず２つ生じるようです。例えば図２の右下図には、左回転する物体の場合を描いています。 左回転する物体には、
- 右手系の左回転する発散トーラス・・・Ｅは（＋）
- 左手系の左回転する発散トーラス・・・Ｅは（－）
の２つが重畳することになります。物体が持つ真のエネルギー値はＥ１とＥ２を合成した値となります。これは如何なる物質や物体でも同じです。
東北大学の早坂秀雄氏による「回転する物体の落下速度」が左右の回転方向によって僅かに異なるという実験は、あったとしても本当に僅かだろうと考えられます。必ず２つの発散トーラスは重畳することによって（＋）（－）が拮抗しているからです。 逆に云えば、２種の発散トーラスの回転を制御してバランスを崩せば物体にかかる真のエネルギー値は変更可能だと云えます。つれて重力は異なってくるはずと考えます。 今のところ具体的にどうすればよいかわかっていません。
陽子・中性子・電子とも図２の右上に示した弧（Ark）を持っていると考えられます。それらすべての発散トーラスを重ねた結果が物体が持つ真のエネルギー値だと考えられます。管理人は、我々が測定可能な物性はすべて「発散トーラスの重ね合わせによる差分」のみだと考えます。電磁気力から重力・核力全ては差分だと考えます。 トム・ベアデンによる手紙にあったヘビサイドが発見したという回転性電磁気エネルギー流を思い出します。
ヘビサイドはまた、比較的⼩さな発散性ポインティング成分に加え、あらゆる電池や発電機の端子から放出される巨大な回転性電磁気エネルギー流を発見しました。このヘビサイド回転成分の大きさは、比較的弱いが発散性であるポインティング・エネルギー流成分よりも1兆倍以上も大きいのです！任意の座標系（特殊相対論の状況）において、回転の発散はゼロです。そのため、通常このヘビサイド成分 – 発電機のシャフトを回す単位時間当たりの機械的エネルギー入力の1兆倍以上 – は、何かと相互作用を起こすことも、また外部回路に発散していくこともありません。代わりに、それはただ空間に向かってうなり続け、浪費されます。
電磁気現象の１兆倍も強いが決して外部に漏れ出さない回転性電磁気エネルギー流と発散トーラスは驚くほど似ています。
いつも引用するある科学者は重力について次のように述べています。
運動している物体のすべては今述べた理由によって周囲に磁場をもっている。つまりあらゆる物質は電子を含んでおり、運動している電子は磁場を作り出す。地球の磁場はその重力場に比べてたいそう弱い。強いフィールドに対する加速が弱いフィールドに反発することによって生じる。
地球の磁場 ＜ 重力場 であると述べています。強いフィールドは重力場を意味し弱いフィールドは地球の磁場を意味します。 置き換えますと次のようになります。
目次
重力場に対する加速が磁場に反発することによって生じる。
これは常識ではありません。ただし、磁場を発散トーラスに置き換えて考えますと意味が違ってきます。
重力場に対する加速は発散トーラスに反発することによって生じる。
「発散トーラスに反発する」とは、図２の左上図に示した接線方向への反発と考えます。つまり、渦流によって物体の真のエネルギー値が決まり、その結果として重力場に対する加速になるということを示しています。このように考えることによって合理的に解釈出来ます。 極小の世界から極大の世界まであらゆる場所において「渦：回転」運動が存在する理由がわかります。
では何故回転するか？ これまで何度も表現してきました。再度書きます。
Ｅ軸上の実体は、投影角９０度の静止した状態に戻ろうとします。すると図２の右上図に示した運動Ｐ３から静止の位置に戻るためには、発散トーラスは無限遠に消失せねばなりません。 言い換えますと、常識的ではない表現になりますが次の通りとなります。
「Ｅ軸上の実体は静止の位置に戻ろうとするが故にＭ軸上の物質は運動せざるを得ない」
陽子・中性子・電子が原子を構成すれば必ず複数の発散トーラスが重畳します。つまり原子は（渦）運動せざるを得ないのです。単独で存在するとき発散トーラスは出ない様です。
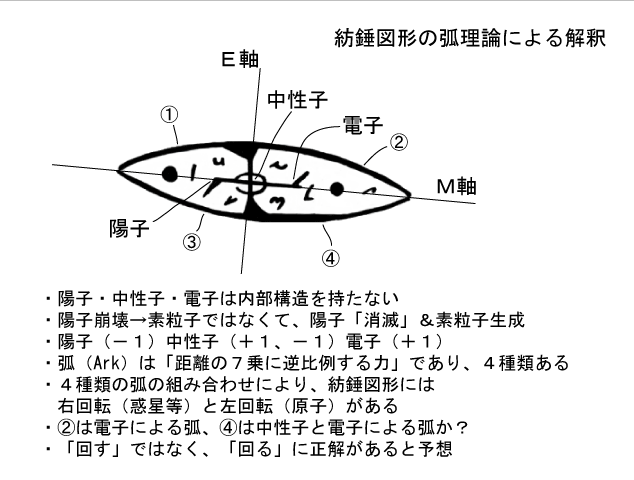図３ 弧理論による原子模型（９０度の部分は１箇所もない）
これまでの自然科学における最大の誤解は、物質とエネルギーを混同していることです。当サイトにおいてエネルギー[ML2T-2]は時間を含むので使えません。運動Ｐと表現しています。すると冒頭で述べたＥ＝ｍｃ２の解釈は次になります。
物質は運動Ｐに転換するし逆にもなるというが、本当は物質も運動Ｐも真のエネルギーを持つ一つの実体が投影されることによって現れる映像に過ぎない。
追記 ２／２０ 上記の説明は少々わかりにくいので追記します。
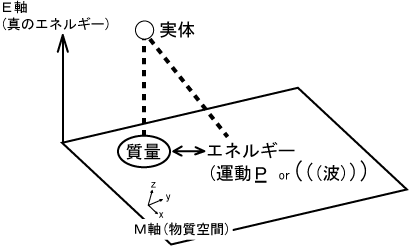図４
特殊相対論のＥ＝ｍｃ２について、物質とエネルギーは等価と解釈されますが、本当は物質もエネルギーも別の次元軸にある実体の投影による映像です。エネルギーは時間を用いずに表現する方法がありませんので、運動Ｐと表現しています。また「波」は、運動の一形態です。そして、発散トーラスは波の一種です。
ニュートリノに質量があるかどうか議論になりますが、ＧｅＶ／ｃ２という質量を表す表現は、質量とエネルギーを混同しているのですから、変なことです。 物質が光速度に近いとき運動Ｐとして現れており、このとき質量はＭ軸において次元を失い測定不能です。 ニュートリノに質量があるかどうかは問題ではなくて、別の次元軸上にある実体が持つ真のエネルギー値を求めることが必要だということです。 ニュートリノやその他の素粒子が波の性質を持つならば、波の質量を云々していることになります。これは奇妙なことです。
一般相対論において、重力は質量による空間の歪みが原因だと説明されています。
図９
質量がエネルギーと等価だとするならば、その解釈で良いですが、質量が原因だというのは間違いです。上記の通り質量は実体が持つ真のエネルギー値が投影されることによって現れますし、実体の投影角が変化することによってエネルギー（運動Ｐ）となりますから、投影角によって質量はＭ軸上で見えなくなります。質量は運動Ｐによって見え方が変わるのですから質量、即重力というのは間違いです。
弧理論 においては、発散トーラスの重ね合わせにより物質が持つ真のエネルギー値が決定します。物質が持つ真のエネルギー値によって重力が決まります。つまり、物質の運動Ｐの状態によって重力は変化するということです。
動画１
物質が持つ真のエネルギー値が変化することによって、例えば動画１に示すアルミホイルや一円玉の様に引力や斥力が働きます。これが重力です。 物質が持つ真のエネルギー値は運動Ｐによって変化します。この運動というのは回転運動（渦）を意味します。
動画２
に示す様に、水面の高さ（真のエネルギー値）は回転運動（渦）によって変化します。この水面の高さ（真のエネルギー値）は、上記の通り発散トーラスの重ね合わせによって決まるということです。
いつも引用するある科学者は、Ｅ＝ｍｃ２の正しい解釈を与える一方で、重力は電磁気現象の一種であると説明しており、相対論による重力の説明は完全に無視しているのは面白いことです。 相対論というのは、原因と結果を時間を使ってうまくすり替えているように思えて、胡散臭く感じます。このようなことで１１０年以上にわたって、方向を違えてきたのですから罪なことです。
Follow me!
