将来、10進法の数学より12進法の数学が便利だと気付かれたならば、一気に増す計算の困難を乗り切る一つのアイディアとしてメモしておきます。
 写真1
写真1
は、昔懐かしい五つ玉そろばんです。これが12進数の計算に使えます。 上の玉は「5」です。下の玉と併せて10になります。 なぜ下の玉が5つのそろばんがあるか調べたところ、こんなのがありました。 一の桁に「10」が揃ったら、一の桁を”払って”10の桁に1を置いたようです。4つ玉のそろばんは、この繰り上がり繰り下がりを暗算することで、1つ玉を減らしたようです。
ここで、12進数の計算を五つ玉のそろばんでやるためには、12進数の一桁暗算が必要になることに気付きます。つまり、「一の桁が揃ったら払って10の桁に1を置く」ためには、6つ玉のそろばんが必要になるということです。
一桁の暗算のために補数を使うことになります。10進数でいえば、
2と8、3と7、4と6、5と5・・・・が補数です。 10進数は、0~9の10個の文字を使いますので、12進数は12個の文字を使います。
今、仮に12進数を0~9と ”a” 並びに ”b” の12個の文字を使って表すとします。
0 1 2 3 4 5 6 7 8 9 a b の後、桁上がりをして「10」となります。青字の10は12進数の10です。 これを5つ玉のそろばんで表すと
 写真2
写真2
となります。(gif が動かないので、以下写真を並べて説明します。)



3~4 の後

5ときて

下の玉5つを払って、上の玉が6になります。続いて7~8ときて

9の次が

aになり、

bときて、

桁上がりして10になります。
ここからが問題です。 まず、12進数の10について、補数を出します。
1ならb 2はa 3は9 4は8 5は7 6は6 ・・・・
例題として、10-1=b 10-2=a なら簡単ですけれど 16-8は?となるともう分かりません。

16と置いて、これが問題です。 えーっと、10を払って、8の補数は4だから

下の玉を4と置く、答えは「a」となります。 では、
21-4は?

まず21と置いて。 4の補数は8だから、10の桁から1引いて、

上の玉6と下の玉2を足して、答えは19です。
これ、例え12進数の電卓があっても使えないことはお分かりいただけることでしょう。いちいち10進に置き換えて考える癖が出てきてしまい混乱します。5つ玉のそろばんなら、なんとかできそうです。
先日の記事に
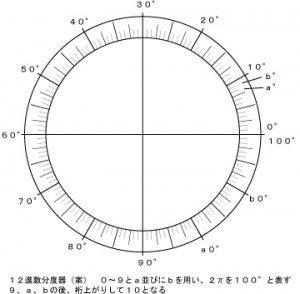
12進数による分度器をあげました。 何が便利なのか、今はピンと来ません。まして12進数の計算となると、何がしたいのかと思われそうです。 以下は例えばの話です。
水H2Oは、摂氏4度で最大密度になり零度で凍ります。非常に多くの物質を溶かし込むことが出来ますし、雪になると
 6角形になります。水の結合は
6角形になります。水の結合は
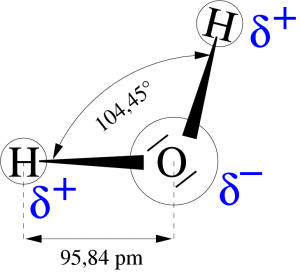
こちらより拝借
104,45°になるようです。この点を質問された方がありまして、こちらに回答されています。 しかし読んでも何かよくわかりません。 ここから当サイトのやりかたです。
物理でいうエネルギーには、時間を含んでいますから、使えません。 我々に分かるのは「運動」だけですから、
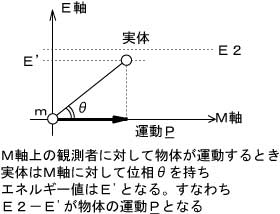
図1
エネルギー[ML^2T^(-2)]を図1の運動Pと言い換えます。E軸上の実体が積分を伴って投影されることで質量を持つ物質が位置を伴って現れます。この投影角θに応じたE軸上の変位(E2-E’)が運動Pとなります。
(1)E2-E’ と(2)θ 並びに(3)運動P(物理でいうエネルギー)の間について、適切に繋げることができれば、つまり、(2)に3次元空間を等しく分けることができる12進数を使い、(3)のエネルギーにかかる定義を適切に扱えば、上記の水が持つ数々の性質を統一的に、理解の容易な形で表せるのではないか?と考えています。



