「軌道電子に働く力」と「単極誘導に生じる力」の違い

このところ考察は止まっていて、思考停止状態です。　弧理論による重力制御の仕組みと単極誘導モーターでの応用について考えています。　重力の何たるかは弧理論として筋が通っているのですけれど、どうも重力とフリーエネルギーが直接関係しているらしいことがわかってきました。

アダムスキーが乗ったスカウトシップは

図１

どうみても単極誘導モーターの応用です。これが直接フリーエネルギーと関係しているらしいのです。ところが単極誘導モーターの同軸三重反転を水銀を使わずに実験する目処が立たなくて立ち往生しています。

.

動画１
迷うところは、弧理論による重力制御の考察のみを書きっぱなしにするか、単極誘導モーターでの実験の可能性について記述するかです。記述するならば実験装置につなげねばならないし、フリーエネルギー装置としての単極誘導モーター案を出せないと具合が悪いのです。　もう少し考えてみます。

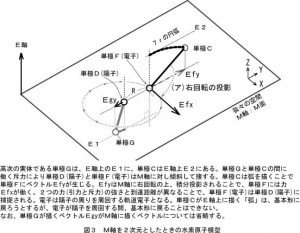
ところで、図１は単極誘導モーターの一種であるとともに、超巨大な単原子と同じ働きをするモーターであろうと考えます。これまでも拙ブログで書いたように「磁石は原子の方向がほぼ揃った巨大な単原子であり、単原子（磁石）の周囲にある自由電子に働く力」が単極誘導の現象だと見られます。

そこで、原子核の周囲にある「軌道電子に働く力」と

図２

磁石の近傍を移動する電子に生じる力の

図３

違いについて書きます。

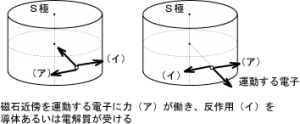
まず、図３の単極誘導モーターの場合について、図３左では磁石の軸に向かって電子が近づくとき軸に直交する向きに力（ア）が働き、その反作用（イ）は電極あるいは電解質が受けます。また図３の右においても同様に力が生じます。単極誘導において作用反作用が必ず成り立っています。

単極誘導モーターにおいて、これまでの実験から生じる力は

・磁石からの距離に反比例する。

・磁石は生じる力と力学的に孤立している。

ことがわかっています。

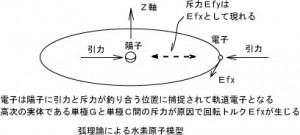
次に図２の原子の軌道電子に働く力について

電気力によって電子は原子核との間に引力が働いています。同時にＥ軸上の実体どうしに働く斥力が（回転する力）としてＭ軸に生じます。（図４参照）

図４

引力と斥力（回転する力）によって電子は軌道電子となっています。　軌道電子の特徴は

・おそらく回転する力は、原子核との距離に逆比例する。

・おそらく原子核は軌道電子に生じる力（回転する力）と力学的に孤立している。

・軌道電子に生じる力（回転する力）は周囲に反作用を受けるべき固定された点が存在しない。

上の２つは管理人による予想ですけれど、単極誘導の実験で得られた結果と同様ではないかと思います。問題は、軌道電子に働く力は、反作用を受けていないということです。　（もちろん、電子が粒子であり、確率的な波であるという考えを捨てています。弧理論はむしろ古典的です。）

反作用を受けるべき相手が存在しないということは、即、求めているフリーエネルギーの仕組みに他なりません。この反作用を受けるべき「何も固定された物がない。絶対静止が存在しない宇宙空間」において、どのようにすれば回転する力を得られるかのアイディアはあります。

 

ヒントは「無限長ソレノイド」です。

図５

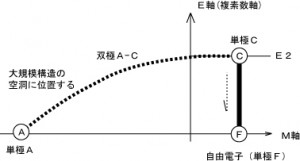
我々が存在する３次元物理空間（Ｍ軸）に直交するエネルギー軸（Ｅ軸）上に実体があり、「積分を伴う回転投影」によって「質量と位置」が決まる。というのが弧理論の基本的な考え方です。　　ただし物理学でいうエネルギー[ML^2T^(-2)]とは異なります。 時間[T]に問題があり、使えないからです。詳しくは右リンク先「弧理論への入り口」あるいは「第３起電力のエネルギー源（第２版）」か「時間」でブログ内検索してください。

図５の単極Ａと単極Ｃ（自由電子Ｆの実体）は「対」をなし双極を形成しています。Ｅ軸上の実体である単極Ａも単極ＣもＭ軸に投影されるまでＭ軸上の位置を特定できません。双極Ａ－ＣはＭ軸に投影されることで単極Ｃは電子（単極Ｆ）になります。　投影の際の条件は

・単極Ａと単極Ｃまたは電子（単極Ｆ）には斥力が働く

・双極は投影される際、片方のみ質量を得る。（双極は物質として現れない。物質が双極であることはない。）

実体である単極Ｃが投影されて電子（単極Ｆ）となり、単極Ｃの「対」である単極Ａは、斥力によって電子から無限遠といえる位置に生じるが、電子のように物質としての性質は持ち得ないと考えます。これは

図６

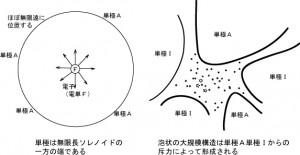
右のように、電子の大きさから見ると無限遠の位置に単極Ａが存在することとなります。また、単極Ａは投影の条件から質量を持ち得ません。これが宇宙の大規模構造をなす原因と考えられます。（図６右の単極Ａと単極Ｉはいわゆる暗黒物質と暗黒エネルギーと呼ばれているものです。）　　物質は泡状の空間から斥力を受けて膜状を形成するわけです。

そして、図６の左のように電子から見ると単極Ａは３次元的に位置を特定できず双極の一方の端である電子（単極Ｆ）は言うなれば「双極の一端」が単極として現れたのであって、電子は無限長ソレノイドの一端だということになります。ただし、ここでいう「無限長ソレノイド」は電磁気学でいう無限長ソレノイドとは異なる概念です。

以上が、拙著「弧電磁気論：現弧理論」のｐ２２～ｐ３０に書いたことです。

ここからは、アイディアです。　　今、まわりに何もない空間に電子が存在し、電子が見えないけれど双極をなし、一方の極が無限遠に位置すると考えます。すると、無限長ソレノイドの回転モーメントは大きくなります。そして、見えないけれど電子が無限長ソレノイドの一方の端を起点に力を生じて反作用を無限長ソレノイドが受けるとします。すると無限長ソレノイドはほとんど動くことはないでしょう。これが宇宙に存在する物質全部で起きると想像してください。

改めて、図６の右を見ます。すべての惑星・恒星・銀河を含むすべての物質が見えない超空洞からの斥力と物質の回転する力の反作用を受けて、渦を巻いているというのが弧理論の考える宇宙像です。

で、単極誘導モーターにおいて、反作用を電子の実体である単極Ｃなりに転嫁できればよいと気づきます。実に奇想天外ですけれど、原子の構造と宇宙の構造は直結しています。それこそが「統一的である」ということだと思います。

この無限長ソレノイドのアイディアは、西遊記の孫悟空が持つ「如意棒」のイメージです。

図７

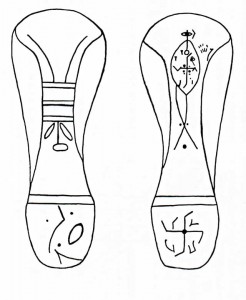
追記１　　我々が宇宙の外に出るという考えは無意味です。 図５によれば、投影された物質でてきた我々がどんなに遠くへ行っても、そこが宇宙だからです。　弧理論によれば投影によって「質量と位置」が決まることが宇宙の定義なのです。図７のようにお釈迦様の掌と孫悟空の両方を見渡せる位置に我々が立つことは不可能です。

弧理論の宇宙を示す

図８

は、宇宙の外についてまったく述べていません。図８の輪郭のどちらが図６右の単極Ａなのか単極Ｉなのかはまだわかっていません。

追記２　無限長ソレノイドのアイディアは、トム・ベアデンが唱える縦波に近いものがあります。スカラー波が存在するとするなら、宇宙の大規模構造と関係するのではないでしょうか。

ブログランキングの応援と広告のクリックをお願いします。