動画サイトに「放電を用いた単極誘導モーターにおける作用と反作用」 を掲載しました。
先日、うまく撮影できなかった放電を用いた単極誘導モーターの力学的特性について、なんとか撮影できましたので、掲載しました。
.
まったく常識通りの結果でした。 一度は確かめる必要がありましたので、これでOKです。
電子の運動にかかる反作用がかなり重い単極誘導モーターを揺らせるのですから結構すごいことです。
ブログランキングの応援と広告のクリックをお願いします。
実験の多くは失敗する訳で、こちらに載せることはないのですけれど、今回の実験は記録しておきます。 うまく行ったかどうかは主観ですから。
今回の実験ですが
放電を用いた単極誘導モーターで、作用と反作用を調べたかったので、モーターを0.2㎜ポリウレタン線で吊り下げました。中心を(-)、外側の金属リングを(+)とする20kv半波整流電圧を印加したものです。 放電は反時計方向に回転します。ポリウレタン線のねじれによって放電の回転に対する反作用を観察しましたが、明確にはわかりませんでした。
吊り下げた銅円板と磁石が前後左右ねじれの静止に5分~10分必要です。 放電を30秒ほどの間継続・切った様子を観察。 反作用によるねじれを明確には判断できませんでした。 放電自体の(曲げ)に要する力は微々たるものですから、別の違ったアイディアによる実験が必要のようです。
以前記録したように
.
地球の自転がジェット気流により維持されていると考えたとき、気流の反作用は「どこかに消え去った」ように見えます。 自転の方向と年間を通して西から東へ吹くジェット気流は真反対で、どう考えても合点がいきません。 そこで、管理人は単極誘導に関する力学的な考察と実験を続けています。
最近思うのですが、地球の自転はひょっとして地球内部のマントル等の対流に起因する可能性を考えています。なぜならジェット気流が(反作用がない)単極誘導であるならば、マントルの対流も(反作用がない)単極誘導に基づいていると仮定しても何ら不自然ではありません。なぜそのように考えるかというと、ジェット気流は気体であって固体に比べて圧倒的に比重が低いからです。 地球の自転に対して抵抗にしかならない大気や海流の動きは地球の自転を遅くするはずです。 どう考えてもジェット気流には何かあります。マントルの対流によって自転が維持されていると考えることは合理的に思えます。
追記
管理人の単極誘導に対する研究の姿勢は、弧理論の考え方からきています。 「磁石は巨大な単原子である」 「単極誘導の現象は、磁石の中心(重心)位置にある原子核と磁石近傍に位置する自由電子との相互作用である」という考えに基づいています。 極微少な原子の世界は「粒子であり波である」という側面は、弧理論の基本である「E軸・M軸平面(エネルギー軸・質量軸)」にて説明可能です(不十分ながら)。 弧理論の考え方は古典的な描像に近いです。 つまり、周囲に確固たる足場がない空間で電子が原子核の周囲を周回しエネルギーを放出せずに安定している仕組み(反作用のない回転運動)は、そのまま単極誘導の現象に現れていると考えています。それが具体的にはジェット気流なのではないかということです。 右リンク先「自然科学から弧理論へ(数学者岡潔:自然科学は間違っている)」を参照ください。
ブログランキングの応援と広告のクリックをお願いします。
昨日の記事にあげた電磁誘導の現象では、力学的に作用・反作用が成り立っているはずだと記しました。 ちょっと調べてみたけれど誰も検証していないようなので、実験してみました。
.
動画1 (電磁誘導における作用と反作用)
管理人は実験が嫌いなのですけれど、結果が予めわかっている実験は安心できます。当初、ネオジム磁石の往復運動一回でコイルが少しは動くと予想していましたけれど、まったく動かないので撮影できないかと思いました。 ネオジム磁石とコイルの動きを同期させればコイルが反作用を受けていることが理解できるので良しとしました。
磁石の運動(力の作用) => 吊されたコイルの運動(力の反作用) + 電磁誘導の起電力 という関係だと理解しています。
動画1の場合、コイルの自重により反作用を受けており、磁石の往復運動に同期することでコイルの振幅が大きくなりました。そして、一部が電磁誘導の起電力となっています。 この現象では、力学的作用反作用は成り立っていることになります。運動の第3法則あるはニュートンの第3法則というようです。
電気磁気学において、なぜ力学的な検証をしていないのか不思議です。皆当たり前すぎて誰もやらないのでしょうね。
ブログランキングの応援と広告のクリックをお願いします。
動画サイトに単極誘導モーター実験1-4を掲載しました。
.
動画1 (実験1-4)
磁石は上面をS極とし、台に固定しています。銅円板は回転軸を(-)、外縁を(+)として、スズメッキ線を使用。 メッキ線が画面向こう側へ弾かれながら振動し、銅円板は時計方向へ回り出します。 常識的に見て銅円板の回転に対する反作用をメッキ線が弾かれることで受けているように見えます。
.
動画2 (実験1-2)
過去に掲載した単極誘導モーター実験1-2です。 磁石は上面をS極とし、銅円板とともに回転できます。 銅円板は回転軸を(-)、外縁を(+)として、スズメッキ線を使用。 動画1と同様にメッキ線は画面向こう側へ弾かれながら振動し、銅円板は時計方向へ回り出します。 こちらも動画1と同様に銅円板の回転に対する反作用をメッキ線が弾かれることで受けているように見えます。
電磁誘導について、力学的な解釈は次の通りだと考えられます。
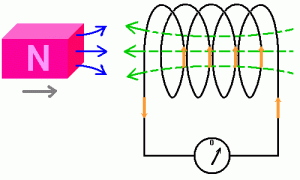 磁石を動かすことでコイルに対して仕事をし、仕事の一部がコイルの誘導起電力となります。 磁石とコイルは接触しません。磁石の運動に対して、(磁力線が介在し)コイルに働きかけます。コイルは(管理人は確かめていませんが)磁石の磁力線から力を受け、置かれた台が反作用を受けているはずです。コイルが(磁力線から)受けた力と台が反作用を受けた差がコイルに誘導起電力として現れます。力学的には、磁石とコイルの間には「磁力線が介在」することで、作用と反作用は成り立っているはずです。 たぶん暗黙の了解なのか、磁石とコイル間の「作用と反作用」を確かめる実験を見たことがありません。 ご存知でしたらお教えください。
磁石を動かすことでコイルに対して仕事をし、仕事の一部がコイルの誘導起電力となります。 磁石とコイルは接触しません。磁石の運動に対して、(磁力線が介在し)コイルに働きかけます。コイルは(管理人は確かめていませんが)磁石の磁力線から力を受け、置かれた台が反作用を受けているはずです。コイルが(磁力線から)受けた力と台が反作用を受けた差がコイルに誘導起電力として現れます。力学的には、磁石とコイルの間には「磁力線が介在」することで、作用と反作用は成り立っているはずです。 たぶん暗黙の了解なのか、磁石とコイル間の「作用と反作用」を確かめる実験を見たことがありません。 ご存知でしたらお教えください。
次に、単極誘導モーターでの力学的な「作用と反作用」について考えます。
動画1では、磁石は固定です。 銅円板に電流が流れたとき、磁力線が介在することで銅円板が回転するならば、磁石が反作用を受けているはずですから、メッキ線が弾かれる理由がわかりません。 何の作用(どういう仕組み・何に対して)メッキ線が弾かれているのか理解できません。
動画2では、磁石は銅円板と一緒に回転しますから、磁力線が介在しても反作用を磁石が受けることで回転することは出来ないはずです。 ここでもメッキ線が弾かれることで銅円板が回転しているように見えます。
動画1と動画2や他の実験においても、メッキ線が弾かれる強さを比較したことはありませんけれど、管理人の経験ではメッキ線が弾かれる強さは、どの実験でも差は感じませんでした。 実験ごとに条件が異なりますので、強さを比較しても意味はありません。 ただ経験的には、単極誘導モーターの回転トルクはメッキ線が受けていると思います。
動画1も動画2も「反作用はメッキ線が受けているように見える」のですが、電磁誘導のように、単極誘導モーターにおいて、どうやったら「磁石と銅円板の間に磁力線が介在し」結果として、メッキ線が反作用を受けることができるのか。管理人には理解できません。
続間違いだらけの物理概念のp137~「磁力線の運動に対する疑問」に次のように書かれています。 「磁力線の速度は定義できない」 し 「要は導体の運動である」と。 まったく、その通りだと思います。 管理人は、観察者と導体円板の相対的な回転運動に起因する。そして、導体円板は磁石の近傍に位置する必要はあるが、磁力線は関係ないと考えています。 これまでの説明は一見正しいように見えるけれど、何かがおかしい。何かが変。
ブログランキングの応援と広告のクリックをお願いします。
放電を用いた単極誘導モーター3を動画サイトに掲載しました。
.
↑(動画1) は
中心の銅円板を電極Aとし、外側の金属リングを電極Bとします。
.
動画2 の
後半、食酢の実験において、中心の磁石を電極Aとし、外側の銅板を電極Bとします。
動画1で、電流の経路は、電極A~放電~電極B 動画2の食酢での電流の経路は、電極A~食酢~電極B です。
動画2の食酢での実験で、管理人は電流の向き(+)(-)を変えたときの違いをきちんと確認していません。たぶん動画1ほどに顕著な違いはなかったと記憶しています。 もっとも食酢は、電気分解で電極に析出があるのと、電流は次第に増加しますので、(+)(-)を変えただけでは同じ条件になりません。(電極を同じ面積で同じ形状の新しい電極に交換が必要です。) ですから、食酢の渦が時計方向と反時計方向で異なるかどうかの判断は難しいです。
はたして、放電以外の単極誘導モーターにおいて、時計方向と反時計方向で回転の強さに差異があるでしょうか。 少なくとも放電を用いた単極誘導モーターは、回転方向によって差異があることは確かです。
ブログランキングの応援と広告のクリックをお願いします。
放電を用いた単極誘導モーターの実験2 を動画サイトに掲載しました。
放電を用いた単極誘導モーター その2
先日公開した
その 1の
動画では、単極誘導モーターの回転軸から給電しました。 今回は、単極誘導モーターである電極Aの外縁部の真横から給電しました。(その2)の画面左上、電極Aの左上45度付近に銅線を接触させたものです。
結果は、1とまったく同じになりました。 事前にわかっていたことながら実際に試した方が納得できます。 巻き込みの強さは、(その2)は(その1)とまったく同じで、かつ時計方向と反時計方向の巻き込みの差も同じでした。
時計方向と反時計方向での巻きのみの差異について、実は9月末に掲載したリポートには、弧理論からの考察を書いていたのですけれど、あまりに奇抜で自信が無かったことから考察を削除して観察結果のみを掲載しました。 実験の進展状況を見て考察の掲載を判断したいと思います。
2014/10/11追記 これまでに、上記の実験と同様(回転方向によって強さに差異がある)の報告をご存知でしたら、コメントかメールでお知らせください。
ブログランキングの応援と広告のクリックをお願いします。解説するサイトですので、繰り返しになります。 実験を始めて来年2月で2年になりますが、管理人が行った一連の実験について時間が経って次第に管理人の思い違いや誤りがあることに気づくとともに理解が深まってまいりました。
.
実験1
は、よく知られた「銅円板と磁石が一緒に回転する」単極誘導モーターです。
電磁誘導は、コイルと磁石の間に磁力線が介在して誘導現象を起こします。力学的にも作用反作用が成り立っていることを実感できます。
ところが実験1は、磁石も銅円板も一緒に回転しますので(力学的に)1.反作用はどこへ行った?2.磁力線が介在しているなら磁力線は空間に固定されているのか?(空間に固定された磁場:磁界が反作用を受けている?)といった疑問がでてきます。 そこで管理人は
.
実験1-2
を行いました。常識的な結果ですけれど、反作用はスズメッキ線が受けていました。メッキ線が弾かれる振動を繰り返した後、ゆっくりと銅円板が回転し始めます。 反作用をスズメッキ線が受けているという観察結果に異論はありませんよね?
式1
は、銅円板と磁石がもつ磁束密度の関係を示しています。 発電機に電流を流すとモーターになるとされますので、式のとおりモーターを解釈するならば「銅円板と磁石」は「磁石の磁力線が介在」して回転することになります。
一方でメッキ線が弾かれる運動は、メッキ線に流れる電流と磁石が持つ磁力線との作用により振動しているとも解釈できます。 あるいは、「単極誘導モーターに生じる力の反作用」+「メッキ線に流れる電流と磁石が持つ磁力線との作用」によるのかも知れません。 この実験では、分離できないと考えられます。
次に行ったのは、
.
実験1-3
です。この実験も実験1-2とおなじで、ただ銅円板を固定したものです。 いくつかの実験を端折りますが
.
実験3
にたどり着きました。ここで特徴的なのは、プラス電極である赤のクリップを銅円板の外縁に取り付けたことです。電流は銅円板の回転軸を通っていません。
実験1-2では、銅円板が回転し始めてメッキ線が弾かれる幅は少し小さくなっています。 しかし、銅円板が固定された実験1-3から幾つかの実験も含め、実験3までにおいて、「メッキ線が弾かれる強さ」に差がありませんでした。 数値化してませんので証明はできないのですが、経験的に差はありませんでした。 メッキ線が弾かれる強さは、銅円板が固定されている状態でプラス端子が回転軸の中心にあっても、外縁にあっても同じ強さだった訳です。 ただし
.
実験3-2
は、メッキ線が銅円板に直接当たっていませんので条件が異なり、同一とは認められません。
結局、メッキ線が弾かれる現象が、「単極誘導モーターに生じる力の反作用」か、「メッキ線と磁力線との作用」なのか、それとも両方が加算されたものなのか判別できません。
一連の実験において、ご意見をくださる方とのやりとりで、管理人が磁石周囲の磁力密度の測定方法を誤っていたことに気づきました。そうすると、磁石中央部において磁束密度がゼロの環境で上記実験を行うことはできないということになります。ということは「単極誘導モーターに生じる力の反作用」と「メッキ線に流れる電流と磁石が持つ磁力線との作用」の両方が加わった結果だと考えて良さそうです。 もっとも「単極誘導モーターに生じる力の反作用」を磁場が受け持っているということを管理人は信じていませんが。
さて、
単極誘導モーターに生じる力の解析の
実験6(動画の3:49~)において、磁石(小)・磁石(中)・磁石(大)での弾かれる強さを比較しました。装置は実験4で用いたもので、電流と電圧は同じ設定です。磁石(小)はネオジム磁石(Φ10×50:576mT:30g)、磁石(中)はアルニコ磁石(Φ20×90:200mT:205g)、磁石(大)はアルニコ磁石(Φ20×150:250mT:368g)です。 いずれも磁石中央部で弾かれる強さを計っています。
結果は、
磁石の強さ(磁極端面での磁束密度:カタログ値)は、 磁石(小)>磁石(大)>磁石(中)
磁石の弾かれる強さは、・・・・・・・・・・・・・・・・・・・・・ 磁石(小)<磁石(中)<磁石(大)
質量は、 ・・・・・・・・・・・・・・・・・・・・・ 磁石(小)<磁石(中)<磁石(大)
装置の設定は同じですから、磁石中央部の磁束密度の違いだけです。弾かれる強さが「単極誘導モーターに生じる力の反作用」と「メッキ線に流れる電流と磁石が持つ磁力線との作用」の両方が加わったものだとしても、「メッキ線に流れる電流と磁石が持つ磁力線との作用」は、磁石の強さに比例するはずです。
「単極誘導モーターに生じる力の反作用」がメッキ線を弾くことがなかったとしても、実験6による「弾かれる強さ」の違いは説明できないと考えます。むしろ、磁石による弾かれる強さの違いは、「単極誘導モーターに生じる力の反作用」が含まれていると考えるのが妥当だと思われます。そして、この結果は、式1をモーターに適用した場合に適合しないのではないかと思います。
初めてご覧の方に。弧理論によれば、「単極誘導モーターに生じる力の強さが磁石の強さ、かつ磁石の質量に比例する」のは、単極誘導の現象が「磁石の原子核と磁石近傍に位置する自由電子の相互作用」だと考えているからです。
以前から聞かされていたことながら、単一の現象として取り出すのは非常に難しいことだと思います。 それにつけても、単極誘導の現象は「(式では)力学的に作用反作用が成り立っていない」ようなのに、百ン十年以上も放置されていることの意味を考えてしまいます。
ブログランキングの応援と広告のクリックをお願いします。
続きです。
いくつかの実験により、単極誘導モーターには、閉じた経路(回路)Lがどのような形であってもスズメッキ線を弾くという形で力を生じると理解しました。 ただし、式1の
![]() 「右辺第1項やローレンツ力」にかかる力も併せて生じることを考慮せねばなりません。
「右辺第1項やローレンツ力」にかかる力も併せて生じることを考慮せねばなりません。
そこで、閉じた経路(回路)Lが持つ線積分ができるだけ小さくなり、かつ、回路の内側の面積Sが小さくなる回路を持つスズメッキ線が弾かれる装置を考えました。
図2-1(1)で、回路Lの(+)からの太い線と細いスズメッキ線の間隔は約13㎜です。
赤い線が(+)で、銅片をポリネジで垂直に設けたアクリル板に取り付けています。
は図2-1(1)の視線から見たもので、スズメッキ線の持つ弾力から「弾かれた力」に比例して湾曲するので、背後に設けた目盛りで弾かれた力の強さがわかります。
アルニコ磁石は実験8に用いたものと同一の製品です。磁石はアルニコ磁石をアクリルの台に乗せて、磁極方向へスライドします。そうすることで、接点を磁石のア・イ・ウの位置へセットすることができます。
前回の記事と同様に実験4が式1に従うと考えて見ます。
図2-2(1)は、横軸が磁石の位置で、縦軸が磁石の磁極方向の磁束密度Bです。重ねて前回記事に示した実験8でのブラシとア・イ・ウの関係を図示しました。 図2-2(2)では、実験4で使う装置のア・イ・ウを書き込んでいます。図2-1(1)に示す(ア)と(ウ)は実験8より磁極に近くなっています。実験8では装置の具合からブラシと(ア)まで、距離がありましたが、実験装置4では、接点の構造上(ア)をS極の角にセットすることができます。(ウ)もN極の角の位置まで磁石をスライドさせることができます。 実験4と実験8の最も大きな違いは、実験4では、閉じた経路(回路)Lが磁石の位置ア・イ・ウによって変化しないことです。つまり、実験4では、回路Lの線積分の値が幅13㎜による回路として固定されていることです。また、回路Lの面積Sも固定です。 ですから、式1に従うとすならば、回路Lは磁石の位置ア・イ・ウによって、磁束密度Bの分布の中の一定幅のみを受けた線積分の値を元に力が生じる(弾かれる)はずです。 (管理人の考え方)
上記の考え方で、図2-2(2)により、スズメッキ線が弾かれる大きさを磁石の位置ア・イ・ウの別で推測しました。 実験装置4の接点に、磁石の(ア:S極)の位置をセットしたとき、回路Lは、磁束密度分布の①と②付近の一部を線積分した値を持ちますので、「①と②の一部+ⅰ」とします。「ⅰ」は、「右辺第1項やローレンツ力にかかる力」の分だと考えます。3つの合計を(ア)の位置に縦棒グラフとして示しました。 次に、磁石の中央部(イ)の位置を接点にセットします。磁石中央部は
のように磁束密度Bがほぼゼロですので、接点が持つ回路Lによる線積分に基づく部分はゼロに近いと考えられます。そこで、 「右辺第1項やローレンツ力にかかる力」の分を「ⅱ」としました。 回路Lを流れる電子は磁束密度が小さい領域から進入し、接点を通って磁束密度が小さい領域を通って電源へ戻るのですから、「ⅱ」は小さいと思われます。 どれ位かわかりませんので、図の様に仮に縦棒グラフを描いてあります。 そして、磁石の(ウ)を接点にセットします。おそらく 「右辺第1項やローレンツ力にかかる力」の分は(ア)と逆方向になると思われますが、よく理解できません。とにかく「ⅲ」と起きます。 ③の領域の回路Lの線積分にかかる分と「ⅲ」を加えた「③の一部+ⅲ」としました。 正直、縦棒グラフをどれだけに描けばよいのかわかりませんでした。
結局、実験4が式1に従うと考えた場合は、図2-2(2)の縦棒グラフのように、(イ)を中心に左右非対称になるのではないかと考えました。
図2-4
に示すように、「W」型になりました。左端は、S極角から10㎜左へ接点を持ってきた時の弾かれた強さです。右端は、N極から10㎜右へ接点を持ってきた時の弾かれた強さです。(イ)の部分が単極誘導モーターに生じる力として現れたものと考えています。 別の実験7(水銀を用いた単極誘導モーター)において、
のように観察しました。 実験7においてS極の(ア)を接点の位置にもってきたときのスナップ写真です。 このとき画面の手前、赤い矢印の先、水銀が盛り上がっている部分が実験4で現れた「弾かれ: 図2-4の(ア)」と同じものだと考えています。
写真2-4
は、実験7においてN極(ウ)を 接点の位置にもってきたときのスナップ写真です。 このとき画面の少し向こう側、赤い矢印の先、水銀が盛り上がっている部分が実験4で現れた「弾かれ: 図2-4の(ウ)」と同じものだと考えています。
写真2-3と写真2-4を見比べると水銀の盛り上がる位置が異なっています。この違いが図2-2の「ⅰ」と「ⅲ」の違いではないかと思います。 つまり、実験4の(ア)と(ウ)において、スズメッキ線は、写真2-2の下方へ弾かれるだけでなく、磁石の磁力線の方向へ「3次元的な」弾かれる運動をしていたのではないかと考えています。しかしながら、当時、磁石が(ア)や(ウ)の位置でスズメッキ線が弾かれる様子を真上から観察しなかったので断言できません。再現はできますが、やってません。
次に、実験7において、磁石を中央部(イ)の位置へ持ってきた場合は、
のようになります。これは、実験4の結果である図2-4(ウ)に相当します。水銀を貯めた容器に渦ができています。
これは、実験2
とまったく同じものだということが理解できます。
結局、実験8は式1に従っていると判断できますが、実験4では式1に従わないと思います。
改めて、単極誘導モーターに生じる力の解析を見ます。 実験5において、アルニコ磁石を縦に置きますと接点にあるスズメッキ線は画面手前方向に弾かれます。動画では省いていますが、磁石をN極・S極逆方向に置くとスズメッキ線は接点の銅片に吸着します。つまり、電源の(+)(-)を逆にすると接点に吸着されるのです。このことは確認済みです。
管理人の結論としては、「単極誘導モーターに生じる力は、磁力線あるいは磁束密度には関係しない」です。
言い換えますと、「単極誘導モーターに生じる力は、磁極の方向(磁石の向き)に関係はあるが、磁力線(磁場・磁界)には関係ない」です。 意味不明だと思いますが、最近、非常に重要なことなのだということがわかってきました。 一般的に、
1.磁力線(磁場・磁界)は磁石にくっついている。
2.磁力線は空間に固定されている。
3.磁力線の速度は定義できない。(1でも、2でなくても説明可能という立場です)
という説明がなされていることが多いです。参考 で、管理人が主張しているのは
4.単極誘導モーターは、磁力線で回るのではない。 1でも2でも3でなく、そもそも磁力線は関係ないという4番目の立場です。
(ただし、単極誘導発電が4.だとは、まだわかりません。)
ブログランキングの応援と広告のクリックをお願いします。
昨年2月から単極誘導に関する一連の実験を始めてから、動画サイトに20本あまりの動画を作成投稿しました。いただいたコメントに十分お答えできなかったので、こちらに記します。 管理人は電磁気学を学ばれた方々が一連の実験を見て、どのようにお考えなのかよく理解できません。勉強されるときは、公式から入って理解を深めるのが一般的だと思います。 管理人は、公式は頭の片隅において、実験の経験でわかった方を優先します。ですから、独りよがりな片寄った考えに陥っているという自覚はあります。コメントをいただくことによって軌道修正できることはありがたいことで感謝しています。 ここでは、管理人が得た結論の一つについて説明します。
実験結果から得た結論、 1.単極誘導モーターに生じる力は「磁力線あるいは磁束密度に関係しない」について。
単極誘導の起電力は 式1
![]() によるとされます。ここで、起電力はV、磁束密度はB、速度はv、半径をL。 Sは、Lを縁とする曲面です。 (注:過去の記事に用いた式1の表記が間違っていました。上記に訂正させていただきます。) 電磁誘導 や ファラデーの円板を参照ください。
によるとされます。ここで、起電力はV、磁束密度はB、速度はv、半径をL。 Sは、Lを縁とする曲面です。 (注:過去の記事に用いた式1の表記が間違っていました。上記に訂正させていただきます。) 電磁誘導 や ファラデーの円板を参照ください。
単極誘導は、軸対称な磁場の同軸上に回転する導体円板の回転軸と外縁に起電力が生じるものです。導体円板は、軸対称な磁場中を運動するので、磁場の強さ磁束密度Bは時間的に変化しません。ですから、式1の右辺第1項はゼロです。右辺第2項は、速度vと磁束密度Bの外積を、閉じた経路Lで線積分します。(注:この解釈でよいのかな?) この右辺第2項が左辺の単極誘導の起電力Vになります。
一般に発電機に電流を流すとモーターになるといわれます。
(1) 単極誘導モーターの一種 実験8 (動画1)
について、式1を適用した場合について考えます。(注:管理人が考えた式1の解釈を実験8に適用したものです。)
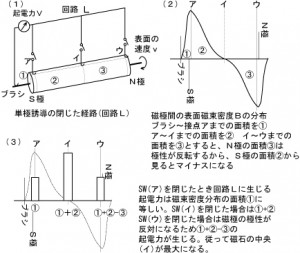 図2
図2
図2(1)は実験8を発電機とした場合を示します。検流計の位置に電源をつなげばモーターになります。 軸対称な磁場を持つ永久磁石を横方向(向かって左をS極、右側をN極)に配置し、回転軸を取り付けます。ブラシにマイナスをつなぎ、ア・イ・ウのいずれかをプラスに接続しますと、回転軸は画面手前方向に回転します。 磁石の閉じた経路(回路)Lは、ブラシ~検流計(電源)を通って、磁石に設けたア・イ・ウを通り~磁石表面~ブラシへ戻ります。実験8では磁石から回転軸への導通が無いため、やむなく磁石に銅の円筒を被せました。ですから多少の磁力線は銅の円筒を通過します。実験8では、銅の円筒の上からテスラメーターにて磁束密度Bを計測しています。(下記図5)
図2(2)は、横軸を磁石の位置(ア・イ・ウ)とし、縦軸を磁束密度Bとしたグラフです。グラフは動画の中でご紹介した(グラフ1:絶対値)の極性を正しく表示したものです。(S極を+、N極を-にしました。) 式1右辺第2項の経路Lにかかる線積分の値は、図2(2)の面積に比例します。
今、モーターとして考えます。 式1において、電源の電圧を一定とし、(経路Lをアとすると)ブラシ~アまでの面積①により、式1右辺第2項の値が決まるので、速度vが定まります。この場合の速度vは回転軸で支えたモーターの回転トルクになります。このモーターの出力が図2(3)アの縦棒グラフです。 次に(経路Lをイとすると)ブラシ~イまでの面積①+②により、式1右辺第2項の値が決まるので、速度vが定まります。このモーターの出力が図2(3)イの縦棒グラフです。 そして、(経路Lをウとすると)ブラシ~ウまでの面積①+②-③により、式1右辺第2項の値が決まるので、速度vが定まります。このモーターの出力が図2(3)ウの縦棒グラフです。 図2(2)において、面積③は②と極性が逆ですから②を③が減ずるところが、この式の要点です。 結果、図2(3)により、実験8において、式1から予想されるモーターの回転出力は、ア<イ>ウ となります。
実際の
実験8の結果は、 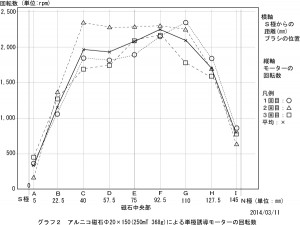 図3
図3
であって、式1と同様の傾向になりました。 普通は、メデタシとなるところですが。
次に 実験4を同じ手法で調べたいと思います。
単極誘導モーターに生じる力の解析 (動画2)
実験4は動画2の途中にあります。
その前に、実験4が単極誘導モーターであることの理解が必要です。 一般に知られている単極誘導モーターは
実験1(動画3)
です。回転する銅板と磁石が一緒に回るモーターで、磁力線が原因で回転すると理解した場合、「どこが、反作用を受けているのか?、磁力線は空間に固定されているのか?」などなど、疑問が出てくる有名な実験です。 電磁誘導のように磁力によって力を受けていると理解すると訳がわからないことになります。
余談ですけれど、磁力線が空間に固定されているか、磁石に?についての見解は、実に様々です。あるサイト(URL失念)では、延々と難しい解説をしていたのを見た記憶があります。
実験1-1 (動画4)
は、何の疑いもなく納得できます。 検索サイトで単極誘導モーター(homopolar motor)関連を調べると上の2つの型が90%を占めます。
管理人が、2013年2月6日最初に行ったのは
実験1-2 (動画5)
でした。反作用をどこが受けているのかを知りたかったからです。勿論、動画5は後日撮ったもので、実際は似たような実験を8種類ほど試しました。(電流の経路をいろいろに変えてみても、スズメッキ線が同様に弾かれることを確認しました。)見ておわかりのように、反作用はブラシであるスズメッキ線が受けています。これが見間違いだと思われる方はありませんよね。 因みに単極誘導モーターに生じる力は接点に生じるという考えを持ったのは、そこからです。
実験1-3 (動画6)
では、 磁石を支えている回転軸を固定するものです。
実験3 (動画7)
で特徴的なのは、モーターの銅板に取り付けた(+)電極がモーターの回転中心を通らなくても弾かれる(単極誘導モーターに力が生じる) ということです。
余談ですけれど、 ということは、単極誘導モーターの近傍にもう一つの回転軸を取り付けたら回転するだろうと考えて
実験2 (動画8)
を試しました。 ずっと後になって、マイケルファラデーが1832年に最初の単極誘導発電機を作ったタイプと同じだとわかりました。
ご承知の通り、この装置は、銅円板が磁力線を横切るので、銅板から見ると磁束密度Bが時間的に変化します。ですから、銅円板に渦電流が生じているだろうとわかります。このタイプの発電機・モーターには反トルクが生じるということです。(恥ずかしながら、まだ、ローレンツ力と式1の右辺第1項との関係がよくわかりません。) ただ、管理人は、磁石のN極とS極の中心には磁力線が存在するのかどうかがなかなか理解できませんでした。
テスラメーターで計ると
中央部に磁束密度がゼロの部分があるのですから不思議です。 とにかく、閉じた経路(回路)Lがどのような形であっても、単極誘導モーターはスズメッキ線を弾くという形で力を生じると理解しました。
長くなりますので次へ続きます。
ブログランキングの応援と広告のクリックをお願いします。研究を始めて、本年末で5年になります。単極誘導モーターの実験は来年2月で2年になります。ン十年前に電磁気学を履修したのは確か週2講義だったと記憶しています。まったく関係のない仕事に就いて以来、ほぼすべて忘れ去りました。当時の計算能力もまったく失いました。今は、電磁気学を”学ぶ”とともに再び”学び直し”ている状態です。
物理学の発達は経済や社会に無縁で純粋に自然への”興味・関心”により発達したと信じるにはナイーブな話しに思えます。 Tom Beaden’s Response to ARPA-E(現在本来のリンク先にあった和訳は切れています) にあるように、1800年代中頃、主にファラデーの研究をまとめた(20の方程式群で表されていた)マクスウェルの原論文は、現在知られている4つのベクトル方程式とは異なります。 ヘビサイドやギブス等が4つの方程式に書き直す過程において、おそらくは当時の研究者たちが大切だと感じていたであろう部分を金融資本家の介入によって削除されたらしい。そうして大学で教えられる電気工学が成立したようです。
上記、トム・ビーデンの手紙によれば、「ヘビサイドはまた、比較的小さな発散性ポインティング成分に加え、あらゆる電池や発電機の端子から放出される巨大な回転性電磁気エネルギーを発見しました。」と、彼が調べた歴史的経緯を述べています。そして、「このヘビサイド回転成分の大きさは、比較的弱いが発散性であるポインティング・エネルギー流成分よりも1兆倍以上も大きい」と言います。
通常、電気磁気の3次元形状は、渦あり(rot)は閉じていて、発散(div)はありません。逆に発散ありは渦なしです。これは双極と単極とに分類されます。 ところが管理人が超効率インバーター「デゴイチ」の第3起電力仮説を考察した「弧電磁気論による第3起電力のエネルギー源についての(考察)」右リンク先から得た結論は、
渦ありでありながら、発散がある右図のようなレンズ状の力場でした。流れが双極の方向に生じて赤道方向へ湾曲し、無限遠に消失するという変わった形をしているらしいのです。格好良く3Dの図形を描けないので申し訳ないのですけれど。考察の結果、レンズ状の力場は上下に分かれており、上半分か下半分しか現れません。同時には現れません。どちらか一方しか現れないようです。
このような力場がトム・ビーデンがいう「回転性電磁気エネルギー」なのではないかと考えています。まったく非常識であることは理解しています。 で、19世紀中頃、マクスウェルやヘビサイド等、当時の実験・理論研究者たちが感じていたであろう意図的に強制的削除された「回転性電磁気エネルギー」はベクトル表記されたマクスウェル方程式からえられた
ところで、歴史的に見て不自然な介入が20世紀初頭にも起きているようです。「師ミラー博士vsシャクランド博士:アインシュタインも関与か!?」 有名なマイケルソン・モーレーの実験でエーテルの存在が否定されました。ところが実験と結果は簡単に結論づけられるようなものではなく、七つの科学事件ファイル「科学論争の顛末」には、1881年に最初の実験が行われ、以後、1905年1924年1925年1933年と続けられました。中には1924年「光の速度のズレを観測した」こともあったが、最終的にはどちらともいえなかったというのが実際のようです。 そころが、もう一つの皆既日食による光の観測で「エディントンによる1919年の実験などの支持も集めて、物理学上の論争は終結を向かえた。」ようです。このエディントンによる1919年の実験とは大きな重力を持つ太陽のそばを通る光は曲げられるか観測するというもので本p104から「星はズレて見えるか?」に詳しいです。太陽のそばを通る星を観測する実験は、「1922年から1952年にかけて起こった10回の皆既日食に際して、引き続き行われた。」 そして、「1952年の時点では、太陽の重力によって生ずる星のズレの値に関する決定的なデータはなく」とあります。 結局、複数回に渡るマイケルソン・モーレーの実験でエーテルの存在は不明確であるにもかかわらず、エディントン等による複数回に渡る皆既日食の観測も1919年の恣意的な観測値を選択した実験で一般相対性理論が正しいと結論づけられたことになります。詳しくは本をお読みください。かなり怪しいです。特にエディントンは。
管理人は、光のエーテルが存在するかどうかの歴史的経緯はともかく、電気磁気現象において、エーテルの存在を意識させるのは「ファラデーの単極誘導」だと思います。3次元空間で足場のないところでいったい何が元で力が伝わるのか。「運動とは何が何に対して運動しているのか」という根本的な問題に気づかされるのが単極誘導だと思います。ご承知の通り光は電気磁気の現象が波として伝わっています。おそらく光より電気磁気の現象の方が身近に扱いやすいと思います。
管理人は、冒頭のとおり電磁気学を”知らない”といってよいでしょう。まして、量子力学や素粒子物理学、相対性理論もわかりません。学生の時、入り口を少々眺めた記憶があります。 しかし、式1を鵜呑みにして、実験を行っている訳ではありません。ですから、理解不足からくる変な解釈もあります。誤解もしています。 ファラデーが単極誘導モーターを考案したのは1821年です。単極誘導発電機を作ったのは1832年のことといいます。10年以上のひらきがあるのです。 発電機・モーターが一般的でない時代において、「同一の原理による異なる面」のものだという認識は当時はなかったと思っています。このような発想からでないと管理人が求めている「非対称性」は見つけられないのではないかと思っています。 自分が実験を行っているにもかかわらず、うまく説明さえできていないことがあります。少しずつ理解を深めてい行きたいと思います。
本日、サイトに掲載した「放電を用いた単極誘導モーターについて」の実験で参考にしたA・D・ムーア著:静電気の話から、p234「静電気学の将来」という文章が印象に残ったので引用します。 管理人は、現代の物理学が数学に偏り過ぎていると感じています。意図して捨て去ったものは身近にあると感じています。
「私が静電気の応用の分野に入ってきてもらいたいと思うのは、特に実験家である。理論家も、すべての原理や、いろいろな理論、必要な数学についてよく知っているという点で、たしかに必要である。ただし、物ごとが理論どおりに単純におこるとしてである。しかし静電気で物ごとはそう単純にはおこらない。電界の形は解析できないほど複雑なこともあるし、コロナ現象はきれいな方程式に簡単にあてはまるほど簡単ではない。ここで―――偉大なファラデーのような―――実験家が登場することによって、時間の節約ができるようになる。実験家も、何の見通しもなく実験するわけではない。彼も多くの原理や効果、現象についての知識をもっている。しかしちがう点はやってみることである。彼はファラデーのように天才的であり、ファラデーのように新しい研究方法を考案する。彼はファラデーのように、新しい道具を自分で作り出す。さらにファラデーのように鋭い観察者で、常に期待していることを探しつづけると同時に、期待していないことも見逃すことはない。また、ファラデーのように、いろいろな現象を物理的に理解し、自分のものにしている。ファラデーのように、いろいろな問題について四六時中考えつづけている。ファラデーのようにあきらめることなく、また、ファラデーのように、しばしば他の人が失敗していることを成功させるスリルを味わうことができる。われわれはもっと多くのファラデーを必要としているのである。」
ブログランキングの応援と広告のクリックをお願いします。